直角三角形斜边中线平分面积吗？含30度角的直角三角形的性质证明来了

直角三角形斜边中线定理

直角三角形斜边中线定理是数学中关于直角三角形的一个定理，具体内容为：如果一个三角形是直角三角形，那么这个三角形斜边上的中线等于斜边的一半。

斜边中线等于斜边一半证明

证明过程如下：

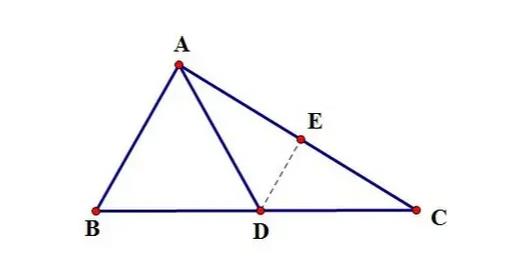
取AC的中点E，连接DE。取BC的中点D

∵AD是斜边BC的中线

∴BD=CD=1/2BC

∵E是AC的中点

∴DE是△ABC的中位线

∴DE//AB(三角形的中位线平行于底边)

∴∠DEC=∠BAC=90°(两直线平行，同位角相等)

∴DE垂直平分AC

∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)

直角三角形的5个性质

(1)直角三角形两个锐角互余;(2)直角三角形斜边上的中线等于斜边的一半;(3)在直角三角形中，30度角所对的直角边是斜边的一半;(4)在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°;(5)在直角三角形中，斜边的一半等於外接圆半径;斜边的中心是外心.

直角三角形斜边逆定理

逆定理：

三角形一边上的中线等于这边的一半，

那么这个三角形是直角三角形。

直角三角形斜边中线平分面积吗?

是。底边相等，高是同一个，所以两个三角形的面积一样。

含30度角的直角三角形的性质证明

30°角所对直角边等于斜边的一半。

分析过程如下：

在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。

证明过程：

Rt△ABC中，∠ACB=90°，∠A=30°，那么BC=AB/2

∵∠A=30°

∴∠B=60°(直角三角形两锐角互余)

取AB中点D，连接CD，根据直角三角形斜边中线定理可知CD=BD

∴△BCD是等边三角形(有一个角是60°的等腰三角形是等边三角形)

∴BC=BD=AB/2

扩展资料：

直角三角形的判定：

1、若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。

2、两个锐角互为余角(两角相加等于90°)的三角形是直角三角形。

3、若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么这个三角形为直角三角形。

4、若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。参考直角三角形斜边中线定理

5、一个三角形30°角所对的边等于某一邻边的一半，则这个三角形为直角三角形。

关键词： 直角三角形斜边中线定理 斜边中线等于斜边一半证明 直角三角形的5个性质 直角三角形斜边逆定理