三角形中心定义是什么？三角形判定的五种方法来了

判断三角形成立的条件有哪些?

可以根据数学公式进行判断。一、数学定理。要构成三角形，必须要任意两边和大于第三边。进行判断的时候，其实只需要判断最小的两边和大于最长一边即可。二、算法设计。根据数学定理，在获取到三个边长后，可以有多种方法进行判断。

判断三条线段能否组成三角形的依据是三角形三边关系的定理：“三角形任何两边的和大于第三边”和它的推论：“三角形任何两边的差小于第三边”。即若三角形的三边是a,b,c，则有：

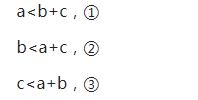
以及

a>c-b(且a>b-c)，④

b>a-c(且b>c-a)，⑤

c>a-b(且c>b-a)。⑥

在具体应用时，一般要在给出的三条线段中，找出一条最长的线段与另两条线段的和进行比较，如果适合定理，另外5个不等式就自然成立。

三角形角度计算方法

1.cosA=b^2+c^2-a^2/2bc或a^2=b^2+c^2-2bccosA;2.cosB=c^2+a^2-b^2/2ca或b^2=c^2+a^2-2accosB;3.cosC=a^2+b^2-c^2/2ab或c^2=a^2+b^2-2abcosC。

三角形

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形(三条边都不相等)，等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

三角形分类

判定法一：

1、锐角三角形：三角形的三个内角都小于90度。

2、直角三角形：三角形的三个内角中一个角等于90度，可记作Rt△。

3、钝角三角形：三角形的三个内角中有一个角大于90度。

判定法二：

1、锐角三角形：三角形的三个内角中最大角小于90度。

2、直角三角形：三角形的三个内角中最大角等于90度。

3、钝角三角形：三角形的三个内角中最大角大于90度，小于180度。

其中锐角三角形和钝角三角形统称为斜三角形。

三角形中心定义

三角形的中心指三角形中心的交点。

重心：三条中线的交点,这点到顶点的距离是它到对边中点距离的2倍;重心分中线比为1：2。

垂心：三角形三条高的交点。

内心：三条角平分线的交点,是三角形的内切圆的圆心的简称; 到三边距离相等。

外心：三条中垂线的交点，是三角形的外接圆的圆心的简称;到三顶点距离相等。

旁心：一条内角平分线与其它二外角平分线的交点。

三角形判定的五种方法

全等三角形的判定方法：“边边边”、“边角边”、“角边角”、“角角边”、“直角、斜边、边”。

1、SSS(边边边)，当三角形的三边对应相等时那么这两个三角形是全等三角形。

2、SAS(边角边)，两边及其夹角对应相等的三角形是全等三角形。

3、ASA(角边角)，两角及其夹边对应相等的三角形全等。

4、AAS(角角边)，两角及其一角的对边对应相等的三角形全等。

5、RHS(直角、斜边、边)，在一对直角三角形中，斜边及另一条直角边相等。

关键词： 判断三角形成立的条件 三角形角度计算方法 三角形中心定义 三角形判定的五种方法